Protocol Design

The Entropy protocol implements a secure 2-party random number generation procedure. The protocol is an extension of a simple commit/reveal protocol. The original version has the following steps:

1. Two parties A and B each randomly sample secret contributions to the random number, $x_A$ and $x_B$.
2. A commits to their number by sharing $h_A = \mathrm{hash}(x_A)$
3. B reveals $x_B$
4. A reveals $x_A$
5. B verifies that $\mathrm{hash}(x_{A}) == h_A$
6. The random number $r = \mathrm{hash}(x_A, x_B)$

This protocol has the property that the result is random as long as either A or B are honest. Honesty means that (1) they draw their value at random, and (2) for A, they keep $x_A$ a secret until step 4. Thus, neither party needs to trust the other -- as long as they are themselves honest, they can ensure that the result $r$ is random.

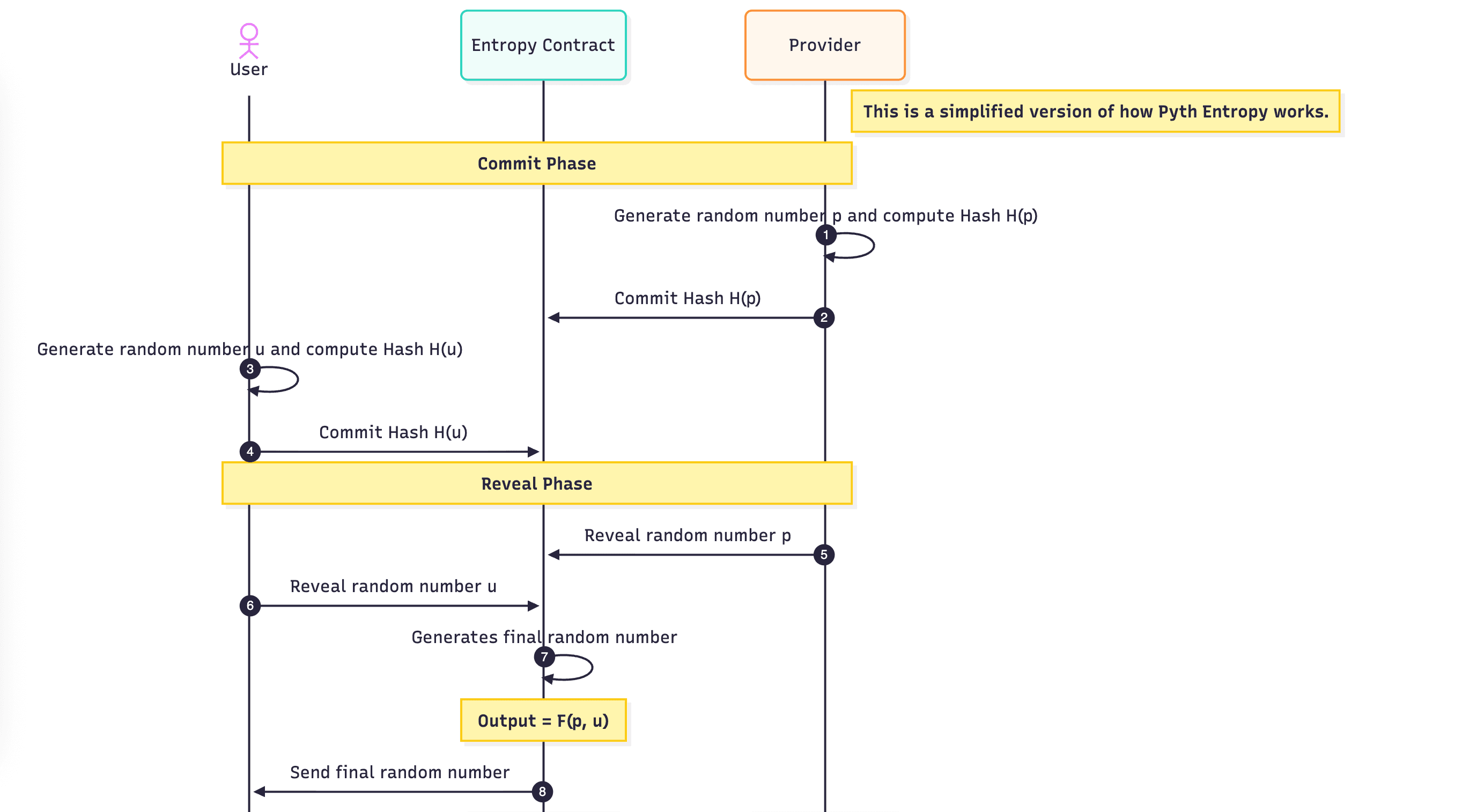
Entropy implements a version of this protocol that is optimized for on-chain usage. The key difference is that one of the participants (the provider) commits to a sequence of random numbers up-front using a hash chain. Users of the protocol then simply grab the next random number in the sequence.

Setup: The provider P computes a sequence of $N$ random numbers, $x_i$ for $0 \leq i \leq N-1$:

• $x_{N-1} = \mathrm{random}()$
• $x_i = \mathrm{hash}(x_{i + 1})$

The provider commits to $x_0$ by posting it to the Entropy contract. Each random number in the sequence can then be verified against the previous one in the sequence by hashing it, i.e., $\mathrm{hash}(x_i) = x_{i - 1}$

Request: To produce a random number, the following steps occur.

1. The user randomly samples their contribution $x_U$ and submits it to the contract. (Users may also run this step using an on-chain PRNG if they trust the validator to not collude with the provider.)
2. The contract remembers $x_U$ and assigns it an incrementing sequence number $i$, representing which of the provider's random numbers the user will receive.
3. After sufficient block confirmations, the provider submits a transaction to the contract revealing their contribution $x_i$ to the contract.
4. The contract verifies $\mathrm{hash}(x_i) == x_{i-1}$ to prove that $x_i$ is the $i$'th random number. The contract stores x_i as the i'th random number to reuse for future verifications.
5. If the condition above is satisfied, the random number $r = \mathrm{hash}(x_i, x_U)$.
6. The contract submits a callback to the calling contract with the random number $r$.

This flow is secure as long as several trust assumptions hold:

• Providers are trusted to reveal their random number $x_i$ regardless of what the final result $r$ is. Providers can compute $r$ off-chain before they reveal $x_i$, which permits a censorship attack.
• Providers are trusted not to front-run user transactions (via the mempool or colluding with the validator). Providers who observe user transactions can manipulate the result by inserting additional reuests or rotating their commitment.
• Providers are trusted not to keep their hash chain a secret. Anyone with the hash chain can predict the result of a randomness request before it is requested, and therefore manipulate the result. This applies both to users of the protocol as well as blockchain validators who can use this information to manipulate the on-chain PRNG or reorder user transactions.

The code of default deployed provider can be found here (opens in a new tab).